RDSAR(距离-多普勒SAR成像算法)
算法概述
RDSAR(Range-Doppler SAR)是一种经典的合成孔径雷达(SAR)成像算法,通过距离-多普勒域处理实现高分辨率雷达图像重建。该算法是SAR成像的基础方法之一,广泛应用于遥感、军事侦察、地形测绘等领域。
MATLAB 实现
%{
本代码用于对雷达的回波数据,利用RD算法~普通版本进行成像。
2023/11/18 20:47
%}
close all;
%% 数据读取
% 加载数据
% 1536*2048 complex int8
echo1 = importdata('CDdata1.mat');
% 1536*2048 complex int8
echo2 = importdata('CDdata2.mat');
% 将回波拼装在一起
% 3072*2048 complex int8
echo = double([echo1;echo2]);
% 加载参数
para = importdata('CD_run_params.mat');
Fr = para.Fr; % 距离向采样率
Fa = para.PRF; % 方位向采样率
f0 = para.f0; % 中心频率
Tr = para.Tr; % 脉冲持续时间
R0 = para.R0; % 最近点斜距
Kr = -para.Kr; % 线性调频率
c = para.c; % 光速
% 以下参数来自课本附录A
Vr = 7062; % 等效雷达速度
Ka = 1733; % 方位向调频率
f_nc = -6900; % 多普勒中心频率
lamda = c/f0; % 波长
%% 图像填充
% 计算参数
[Na,Nr] = size(echo);
% 按照全尺寸对图像进行补零
% 4096*3414 complex double
echo = padarray(echo,[round(Na/6), round(Nr/3)]);
% 计算参数
% 4096*3414 complex double
[Na,Nr] = size(echo);
%% 轴产生
% 距离向时间轴及频率轴
tr_axis = 2*R0/c + (-Nr/2:Nr/2-1)/Fr; % 距离向时间轴
fr_gap = Fr/Nr;
% 交换行向量的左右两半部分。如果一个向量的元素数为奇数,则中间的元素被视为属于向量的左半部分
fr_axis = fftshift(-Nr/2:Nr/2-1).*fr_gap; % 距离向频率轴
% 方位向时间轴及频率轴
ta_axis = (-Na/2:Na/2-1)/Fa; % 方位向时间轴
ta_gap = Fa/Na;
fa_axis = f_nc + fftshift(-Na/2:Na/2-1).*ta_gap; % 方位向频率轴
% 方位向对应纵轴,应该转置成列向量
ta_axis = ta_axis';
fa_axis = fa_axis';
%% 第一步 距离压缩
% 距离向傅里叶变换,返回每行的FFT计算结果
echo_s1 = fft(echo,[],2);
% 距离向距离压缩滤波器
echo_d1_mf = exp(1i*pi/Kr.*fr_axis.^2);
% 距离向匹配滤波,返回每一行的 n 点逆变换
echo_s1 = ifft(echo_s1 .* echo_d1_mf,[],2);
%% 第二步 方位向傅里叶变换&距离徙动矫正
% 方位向下变频
echo_s1 = echo_s1 .* exp(-2i*pi*f_nc.*ta_axis);
% 方位向傅里叶变换,返回每一列的FFT计算结果
echo_s2 = fft(echo_s1,[],1);
% 计算徙动因子
D = lamda^2*R0/8/Vr^2.*fa_axis.^2;
G = exp(4i*pi/c.*fr_axis.*D);
% 校正
echo_s2 = echo_s2.* G;
%% 第三步 方位压缩
% 方位向滤波器
echo_d3_mf = exp(-1i*pi/Ka.*fa_axis.^2);
% 方位向脉冲压缩
echo_s3 = echo_s2 .* echo_d3_mf;
% 方位向逆傅里叶变换,返回每一列的逆变换结果
echo_s3 = ifft(echo_s3,[],1);
%% 数据最后的矫正
% 根据实际观感,方位向做合适的循环位移
echo_s4 = circshift(abs(echo_s3), -3328, 1);
% 上下镜像
echo_s4 = flipud(echo_s4);
echo_s5 = abs(echo_s4);
saturation = 50;
echo_s5(echo_s5 > saturation) = saturation;
%% 成像
% 绘制处理结果热力图
figure;
imagesc(tr_axis.*c,ta_axis.*c,echo_s5);
title('处理结果(RD算法)');
% 以灰度图显示
echo_res = gather(echo_s5 ./ saturation);
% 直方图均衡
echo_res = adapthisteq(echo_res,"ClipLimit",0.004,"Distribution","exponential","Alpha",0.5);
figure;
imshow(echo_res);
MindSpore Signal+ 实现
在开始编写 MindSpore Signal+ 实现之前,建议先对原始 MATLAB 代码做流程梳理。可以将整体算法分为以下几个部分:
1.数据读取
2.数据预处理
3.核心计算
4.数据后处理
1. 数据读取
在matlab中,数据读取是通过importdata函数实现的。在Python中使用MindSpore Signal+时,我们可以使用NumPy的loadmat或SciPy的io.loadmat来加载MATLAB文件中的变量,因此在Python代码开头需要导入NumPy和SciPy。
示例代码:
# step 0 : 准备初始数据
echo1 = np.array(sio.loadmat('CDdata1.mat')['data'])
echo2 = np.array(sio.loadmat('CDdata2.mat')['data'])
echo = np.append(echo1, echo2, axis=0)
# print(echo.shape)
# RD-SAR parameters
para = sio.loadmat('CD_run_params.mat')
备注
如果当前Python环境中没有安装scipy.io,可以通过pip进行安装:pip install scipy
2. 数据预处理
从算法整体分析,数据读取后到核心计算之前的步骤,主要是对数据进行填充和轴的生成,这部分都是核心计算的前期准备,建议将这部分代码封装在__init__函数中完成,不放在construct函数中可以避免额外的开销,当实例化一个类时自动触发一次__init__函数。
示例代码:
class rdsar(nn.Cell):
# 数据预处理
def __init__(self, echo_shape, para, Ka, f_nc):
super(rdsar, self).__init__()
self.Fr = para["Fr"][0][0]
# 方位向采样率
self.Fa = para["PRF"][0][0]
# 中心频率
self.f0 = para["f0"][0][0]
# 脉冲持续时间
self.Tr = para["Tr"][0][0]
# 最近点斜距
self.R0 = para["R0"][0][0]
# 线性调频率
self.Kr = -para["Kr"][0][0]
...
# 核心计算
def construct(self, inputs):
...
return results
3. 核心计算
核心计算部分是算法的核心,也是计算复杂度最高的部分,建议将这部分代码封装在construct函数中,这样可以方便后续的调用。核心计算的迁移主要是将matlab的计算逻辑转换为MindSpore Signal+的API调用,例如:matlab中的fft(echo,[],2)可以转换为mr.FFT(dim=1),dim=1 表示按行计算(沿着列移动,计算每行的FFT)。MindSpore Signal+ API列表可以查阅MindSpore官方文档和自定义算子列表。
示例代码:
class rdsar(nn.Cell):
# 数据预处理
def __init__(self, echo_shape, para, Ka, f_nc):
...
self.fft = mr.FFT(dim=0)
self.fft1 = mr.FFT(dim=1)
self.ifft = mr.IFFT(dim=0)
self.ifft1 = mr.IFFT(dim=1)
...
def construct(self, echo, temp, temp1, temp2, temp3):
echo = self.cast(echo, ms.complex64)
echo_s1 = self.fft1(echo)
echo_d1_mf = ops.exp(self.sq_fr_axis * temp)
echo_s1 = self.ifft1(echo_s1 * echo_d1_mf)
echo_s1 = echo_s1 * ops.exp(temp1 * self.ta_axis)
echo_s2 = self.fft(echo_s1)
...
return echo_s5
小技巧
1.对于一些基本运算符,例如:*,+,/等,只要matlab语义与Python是一致的可以直接写不用转换成API调用。
2.如果某个API在计算流程中反复使用,可以提前在__init__中实例化,减少开销。
完成核心计算部分的迁移后,就可以利用实际输入数据进行测试,验证算法的正确性。
示例代码:
# 准备数据
echo1 = np.array(sio.loadmat("CDdata1.mat")["data"])
echo2 = np.array(sio.loadmat("CDdata2.mat")["data"])
echo = np.append(echo1, echo2, axis=0)
# 图像填充
Na, Nr = echo.shape
echo = np.pad(echo, ((round(Na / 6), round(Na / 6)), (round(Nr / 3), round(Nr / 3))))
new_shape = (4096, 4096)
echo = np.pad(
echo,
((0, new_shape[0] - echo.shape[0]), (0, new_shape[1] - echo.shape[1])),
"constant",
constant_values=0,
)
Na, Nr = echo.shape
echo = Tensor(echo)
para = sio.loadmat("CD_run_params.mat")
Kr = -para["Kr"][0][0]
c = para["c"][0][0]
Ka = 1733
f_nc = -6900
temp = Tensor(np.pi / Kr * 1j, dtype=ms.complex64)
temp1 = Tensor(-2j * np.pi * f_nc, dtype=ms.complex64)
temp2 = Tensor(4j * np.pi / c, dtype=ms.complex64)
temp3 = Tensor(-1j * np.pi / Ka, dtype=ms.complex64)
# 实例化模型
model = rdsar(echo.shape, para, Ka, f_nc)
echo_s5 = model(echo, temp, temp1, temp2, temp3)
print(echo_s5)
4. 数据后处理
需要对计算结果进行成像,这部分主要是将计算结果转换为图像,可以使用matplotlib库进行绘制。
示例代码:
import matplotlib.pyplot as plt
# 成像
print("show image")
plt.pcolor(echo_s5.numpy())
plt.show()
plt.savefig('v3.jpg')
备注
如果当前Python环境中没有安装matplotlib,可以通过pip进行安装:pip install matplotlib
结果对比:
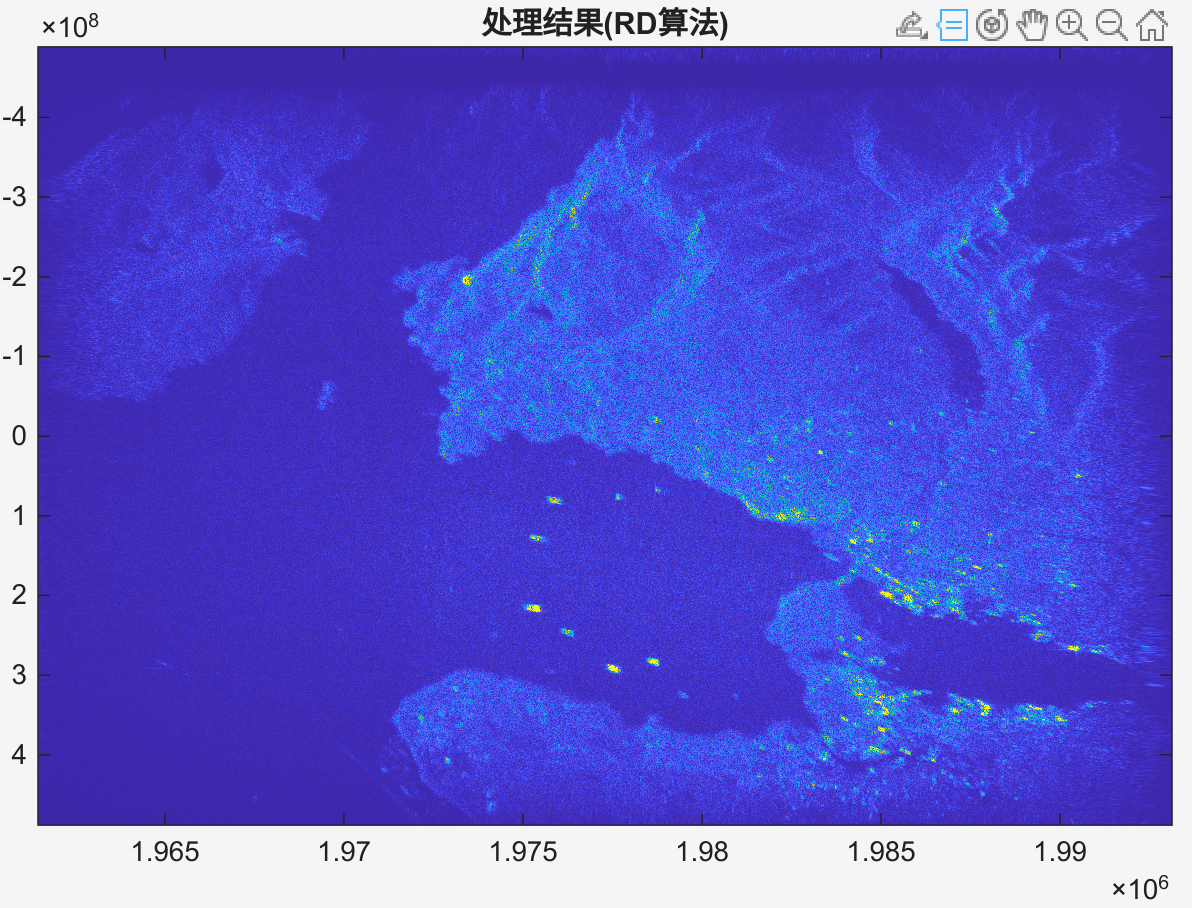
图1:MATLAB结果

图2:MindSpore Signal+结果
可以看出成像上存在一定误差,但整体趋势一致。确认结果无误后,可通过 mindspore.export 导出 MINDIR 模型,便于在 MindSpore Lite 端部署(板卡侧运行)。
以下是完整的MindSpore Signal+实现的代码:
import mindspore as ms
import numpy as np
import scipy.io as sio
from mindspore import Tensor, nn, ops
import mindradar as mr
import matplotlib.pyplot as plt
class rdsar(nn.Cell):
def __init__(self, echo_shape, para, Ka, f_nc):
super(rdsar, self).__init__()
# 距离向采样率
self.Fr = para["Fr"][0][0]
# 方位向采样率
self.Fa = para["PRF"][0][0]
# 中心频率
self.f0 = para["f0"][0][0]
# 脉冲持续时间
self.Tr = para["Tr"][0][0]
# 最近点斜距
self.R0 = para["R0"][0][0]
# 线性调频率
self.Kr = -para["Kr"][0][0]
# 光速
self.c = para["c"][0][0]
# 等效雷达速度
self.Vr = 7062
# 方位向调频率
self.Ka = Ka
# 多普勒中心频率
self.f_nc = f_nc
# 波长
self.lamda = self.c / self.f0
self.saturation = 50
self.Na = echo_shape[0]
self.Nr = echo_shape[1]
self.fr_axis = Tensor(np.arange(-self.Nr / 2, self.Nr / 2), dtype=ms.float32)
self.fa_axis = Tensor(np.arange(-self.Na / 2, self.Na / 2), dtype=ms.float32)
self.fr_gap = self.Fr / self.Nr
self.ta_axis = Tensor(
np.arange(-self.Na / 2, self.Na / 2) / self.Fa, dtype=ms.float32
)
self.ta_gap = self.Fa / self.Na
self.cast = ops.Cast()
self.matmul = ops.MatMul(False, True)
self.fft = mr.FFT(dim=0)
self.fft1 = mr.FFT(dim=1)
self.ifft = mr.IFFT(dim=0)
self.ifft1 = mr.IFFT(dim=1)
self.abs = mr.ComplexAbs()
# 预处理
self.fr_axis = mr.fftshift(self.fr_axis) * self.fr_gap
self.fa_axis = mr.fftshift(self.fa_axis) * self.ta_gap + self.f_nc
self.ta_axis = ops.unsqueeze(self.ta_axis, dim=1)
self.fa_axis = ops.unsqueeze(self.fa_axis, dim=1)
self.D = ops.square(self.fa_axis) * (
self.lamda**2 * self.R0 / 8 / self.Vr**2
)
self.G = self.matmul(self.D, ops.unsqueeze(self.fr_axis, dim=1))
self.sq_fa_axis = ops.square(self.fa_axis)
self.sq_fr_axis = ops.square(self.fr_axis)
def construct(self, echo, temp, temp1, temp2, temp3):
echo = self.cast(echo, ms.complex64)
echo_s1 = self.fft1(echo)
echo_d1_mf = ops.exp(self.sq_fr_axis * temp)
echo_s1 = self.ifft1(echo_s1 * echo_d1_mf)
echo_s1 = echo_s1 * ops.exp(temp1 * self.ta_axis)
echo_s2 = self.fft(echo_s1)
G = self.G * temp2
G = ops.exp(G)
echo_s2 = ops.multiply(echo_s2, G)
echo_d3_mf = ops.exp(self.sq_fa_axis * temp3)
echo_s3 = ops.multiply(echo_s2, echo_d3_mf)
echo_s3 = self.ifft(echo_s3)
echo_s4 = ms.numpy.roll(self.abs(echo_s3), shift=-3328, axis=0)
echo_s4 = ops.flip(echo_s4, dims=[0])
saturation_tensor = ops.full(echo_s4.shape, self.saturation, dtype=ms.float32)
echo_s5 = ops.where(echo_s4 > self.saturation, saturation_tensor, echo_s4)
return echo_s5
# step 0 : 准备初始数据
echo1 = np.array(sio.loadmat("CDdata1.mat")["data"])
echo2 = np.array(sio.loadmat("CDdata2.mat")["data"])
echo = np.append(echo1, echo2, axis=0)
# 图像填充
Na, Nr = echo.shape
echo = np.pad(echo, ((round(Na / 6), round(Na / 6)), (round(Nr / 3), round(Nr / 3))))
new_shape = (4096, 4096)
echo = np.pad(
echo,
((0, new_shape[0] - echo.shape[0]), (0, new_shape[1] - echo.shape[1])),
"constant",
constant_values=0,
)
Na, Nr = echo.shape
echo = Tensor(echo)
para = sio.loadmat("CD_run_params.mat")
Kr = -para["Kr"][0][0]
c = para["c"][0][0]
Ka = 1733
f_nc = -6900
temp = Tensor(np.pi / Kr * 1j, dtype=ms.complex64)
temp1 = Tensor(-2j * np.pi * f_nc, dtype=ms.complex64)
temp2 = Tensor(4j * np.pi / c, dtype=ms.complex64)
temp3 = Tensor(-1j * np.pi / Ka, dtype=ms.complex64)
model = rdsar(echo.shape, para, Ka, f_nc)
ms.export(
model, echo, temp, temp1, temp2, temp3, file_name="rdsarv3", file_format="MINDIR"
)
echo_s5 = model(echo, temp, temp1, temp2, temp3)
print(echo_s5)
# 成像
print("show image")
plt.pcolor(echo_s5.numpy())
plt.show()
plt.savefig('v3.jpg')
板卡部署
模型部署建议使用 YHFT-IDE,它集成了模型转换、模型可视化与 MindSpore Lite 端部署模板。具体使用方法可参考 HelloDSP MindSpore Lite端。
小技巧
源数据为 .mat 格式,C++ 侧无法直接读取。可使用第三方库 MATIO 读取,或先用 Python 转存为通用二进制/文本格式再在 C++ 侧读取。
参考与源码
基于RD、CS和ωk算法的合成孔径雷达成像算法原理与实现:SAR_imaging_with_RD_CS_wk
Python 示例:RDSAR
Lite 端工程:RDSAR